Рассмотрим коэффициент Шарпа — один из основных показателей, используемых для оценки эффективности финансовых активов с поправкой на риск.
Всегда есть искушение рассматривать годовую доходность торговли как самый главный показатель. Однако, появляется много проблем, если рассматривать исключительно этот параметр. Не всегда бывает просто получить цифры доходности некоторых стратегий. Это особенно верно для ненаправленных стратегий, использующих плечо. Эти факторы делают сложным сравнение двух стратегий, основываясь только на их доходности. Кроме того, если у нас есть две стратегии с одинаковой доходностью, как узнать, какая содержит больше риска? Далее, что мы вообще можем понимать под “больше риска”? В финансах, мы часто озабочены волатильностью результатов и периодами просадки. Таким образом, если одна из этих стратегий имеет значительно большую волатильность результатов, она будет менее привлекательна для нас, несмотря на то, что их исторические доходности могут быть похожими или идентичными.
Эти проблемы в сравнении стратегий и оценке риска побуждают использовать коэффициент Шарпа.
Определение коэффициента Шарпа
William Forsyth Sharpe — лауреат Нобелевской премии, экономист, кто создал модель ценообразования активов CAPM и предложил коэффициент Шарпа в 1966 (с обновлением в 1994).
Коэффициент Шарпа определяется по следующей формуле:
Коэффициент сравнивает среднее от превышений результатов стратегии над бенчмарком со стандартным отклонением этих превышений. То есть меньшая волатильность результатов даст нам больший коэффициент Шарпа при той же доходности.
Использование бенчмарка
Формула коэффициента Шарпа предполагает использование бенчмарка. Бенчмарк используется как предел, который конкретная стратегия должна превзойти, чтобы имело смысл ее рассматривать. Например, простая стратегия “только лонг” для акций большой капитализации США должна надеяться в среднем преодолеть индекс S&P 500 или сравниться с ним по доходности при меньшей волатильности.
Выбор бенчмарка может быть неочевидным делом. Например, должен ли ETF сектора быть использован как бенчмарк для индивидуальной акции или лучше взять сам S&P 500? Почему не Russel 3000? Или должна ли стратегия хедж фонда сравниваться с индексом рынка или индексом хедж фондов? Есть еще сложности с “безрисковой ставкой”. Использовать ли национальные правительственные долговые бумаги? Корзину международных долговых бумаг? Краткосрочные или долгосрочные ноты? Смесь? Ясно, что способов выбора бенчмарка очень много. Коэффициент Шарпа использует обычно безрисковую ставку и часто для стратегий на акциях США она основана на 10-летних правительственных казначейских облигациях.
В отдельном случае маркет-нейтральных стратегий есть сложность с вопросом использовать в качестве бенчмарка безрисковую ставку или же ноль? Индекс рынка не может быть использован здесь, т.к. стратегия по определению маркет-нейтральна. Корректный выбор для маркет-нейтрального портфеля — не вычитать безрисковую ставку, поскольку он само-финансируется. Поскольку вы зарабатываете проценты Rf от держания маржи, реальное вычисление результата таково:
(Ra + Rf) — Rf = Ra.
Стало быть не нужно вычитать безрисковую ставку для доллар-нейтральных стратегий.
Ограничения
Несмотря на широкое использование в количественных финансах, коэффициент Шарпа имеет ограничения.
Во-первых, коэффициент Шарпа опирается на прошлые данные. Он считается по распределению исторических результатов и волатильности, а не по тому, что случится в будущем. Когда оценка делается по коэффициенту Шарпа, неявно принимается, что будущее будет похоже на прошлое. Это, очевидно, не всегда так, особенно когда меняются рыночные условия.
Вычисление коэффициента Шарпа предполагает, что используемые результаты имеют нормальное распределение (по Гауссу). К сожалению, рынки часто подвержены эксцессу более высокому, чем у нормального распределения. Поэтому распределения результатов имеют “тяжелые хвосты” и экстремальные события случаются чаще, чем это предполагается распределением Гаусса. Значит, коэффициент Шарпа плохо оценивает хвостовой риск.
Это явно видно по стратегиям, подверженным такому риску. Например, продажа колл-опционов (известная, как “ловля монет под паровым катком”). Постоянный поток опционных премий от продажи колл-опционов приводит к низкой волатильности результатов с хорошим превышением над бенчмарком. Стратегия будет обладать высоким коэффициентом Шарпа (основываясь на исторических данных). Однако она не принимает во внимание, что опцион когда-нибудь может быть исполнен, что приведет к значительной и внезапной просадке (или даже обнулению) кривой эквити. Таким образом, как и с любой другой оценкой алгоритмических торговых стратегий, коэффициент Шарпа не может использоваться изолированно.
Хотя эта мысль может быть довольно очевидной для некоторых, транзакционные издержки ДОЛЖНЫ включаться в вычисление коэффициента Шарпа для реальной оценки. Есть бесконечное число примеров, когда стратегия, имеющая высокий коэффициент Шарпа (и значит похожая на высокодоходную) превращается в систему с низким Шарпом, как только в нее включаются реалистичные торговые издержки. Значит нужно использовать полные результаты для вычисления превышения над бенчмарком и включать туда транзакционные издержки.
Предостережения по использованию коэффициента Шарпа.
Коэффициент Шарпа является основой оценки эффективности финансовых активов. Но необходимо сделать два предостережения относительно его использования: одно связано с интерпретацией отрицательных коэффициентов Шарпа, а другое — с концептуальными ограничениями.
Финансовая теория говорит нам, что в долгосрочной перспективе инвесторам следует компенсировать дополнительную среднюю доходность сверх безрисковой ставки для принятия дополнительного риска, по крайней мере, если рискованный портфель хорошо диверсифицирован. Если инвесторы получат такую компенсацию, числитель коэффициента Шарпа будет положительным.
Тем не менее, мы часто обнаруживаем, что портфели демонстрируют отрицательные коэффициенты Шарпа, когда соотношение рассчитывается за периоды, в которых доминируют медвежьи рынки акций. Это повышает осторожность при работе с отрицательными коэффициентами Шарпа.
| При работе положительными коэффициентами Шарпа, коэффициент Шарпа для портфеля уменьшается, если мы увеличиваем риск, при прочих равных условиях. |
Этот результат является интуитивно понятным для оценки эффективности с поправкой на риск. Однако при отрицательных коэффициентах Шарпа увеличение риска приводит к увеличению коэффициента Шарпа в цифровом выражении (например, удвоение риска может увеличить коэффициент Шарпа с -1 до -0,5).
| Поэтому, сравнивая портфели с отрицательными коэффициентами Шарпа, мы обычно не можем считать, что больший коэффициент Шарпа (тот, который ближе к нулю) означает лучшую эффективность с поправкой на риск.
Однако, если стандартные отклонения равны, портфель с отрицательным коэффициентом Шарпа, близким к нулю, имеет преимущество. |
На практике, чтобы сделать интерпретируемое сравнение с использованием коэффициента Шарпа, нам может потребоваться увеличить период оценки так, чтобы один или несколько коэффициентов Шарпа стали положительными. Финансовый аналитик также может рассмотреть возможность использования другого показателя для оценки эффективности.
Концептуальное ограничение коэффициента Шарпа состоит в том, что он учитывает только один аспект риска — стандартное отклонение доходности. Стандартное отклонение является наиболее подходящим показателем риска для портфельных стратегий с приблизительно симметричным распределением доходности. Стратегии с опционными элементами имеют асимметричную доходность.
Соответственно, инвестиционная стратегия может приносить частые небольшие выгоды, но потенциально может привести к нечастым, но чрезвычайно большим убыткам. Это утверждение описывает обратное распределение с отрицательной асимметрией. Мы обсудим асимметрию позже.
Такая стратегия иногда образно описывается как «собирание монет перед бульдозером». Например, некоторые стратегии хедж-фондов имеют тенденцию к подобной модели доходности.
Рассчитанный за период, в течение которого работает стратегия (т.е. больших убытков не произошло), этот тип стратегии будет иметь высокий коэффициент Шарпа. В этом случае коэффициент Шарпа дал бы слишком оптимистичную картину показателей, скорректированных с учетом риска, поскольку стандартное отклонение не полностью измеряет принимаемый инвесторами риск.
Поэтому, прежде чем применять коэффициент Шарпа для оценки работы менеджера, мы должны оценить, адекватно ли описывает стандартное отклонение риск инвестиционной стратегии менеджера.
Приведенный ниже пример иллюстрирует вычисление коэффициента Шарпа в контексте оценки эффективности портфеля.
Практическое использование и примеры
Очевидный вопрос, на который пока статья не дала ответа “Какой коэффициент Шарпа должен быть у хорошей торговой стратегии?”. В реальности, лучше не использовать стратегии с S<1 с учетом транзакционных издержек. Количественные хедж фонды склонны отказываться от стратегий с S<2. Один известный количественный хедж фонд, с которым я знаком, не будет рассматривать стратегии с S<3. Как розничный алготрейдер, если вы сможете достичь S>2, это будет неплохо. Шарп часто растет с увеличением частоты торговли. Некоторые высокочастотные стратегии будут иметь Шарп до 10 или даже выше, поскольку они могут быть доходными каждый день и конечно каждый месяц. Такие стратегии редко подвергаются катастрофическим рискам и это уменьшает волатильность их результатов, что приводит к таким высоким значениям коэффициента Шарпа.
Но реально такие цифры очень большие, потому что если взять и посмотреть реальный пример, увидим какой может быть коэффициент.
Возьмем данные двух взаимных фондов, Selected American Shares (SLASX) и T.Rowe Price Equity Income (PRFDX), за период 2003г.-2012г.
| Фонд | Среднее арифметическое (%) | Стандартное отклонение доходности (%) |
| SLASX | 8.60 | 20.02 |
| PRFDX | 8.91 | 18.12 |
30-дневная ставка казначейских векселей (T-Bill) США часто используется в качестве безрисковой ставки. Рассчитанная ранее в Таблице среднегодовая доходность Т-Bill за период 2003-2012 годов составляла 1.58%.
Используя информацию из Таблицы 25 и среднегодовую доходность 30-дневных T-Bill, сделайте следующее:
1. Рассчитайте коэффициенты Шарпа для SLASX и PRFDX в течение периода 2003-2012 гг.
2. Укажите, какой фонд имел лучшие показатели с поправкой на риск в течение этого периода, в соответствии с коэффициентом Шарпа.
Решение для части 1:
У нас уже есть средние значения и стандартные отклонения доходности портфеля, а также среднегодовая безрисковая норма доходности с 2003 по 2012 год.
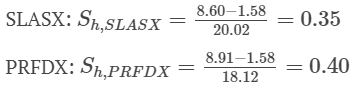
Решение для части 2:
У PRFDX был более высокий положительный коэффициент Шарпа, чем у SLASX в течение рассматриваемого периода. По коэффициенту Шарпа эффективность PRFDX была выше.
Это неудивительно, так как PRFDX имел более высокую доходность и более низкое стандартное отклонение, чем SLASX.
Вы уже сейчас можете начать изучать Видео курс- роботы в TSLab и научиться самому делать любых роботов!
Можно записаться на следующий поток ОнЛайн курса «Создание роботов в TSLab без программирования», информацию по которому можно посмотреть тут->
Также можете научиться программировать роботов на нашем Видео курсе «Роботы для QUIK на языке Lua»
Если же вам не хочется тратить время на обучение, то вы просто можете выбрать уже готовые роботы из тех, что представлены у нас ДЛЯ TSLab, ДЛЯ QUIK, ДЛЯ MT5, ДЛЯ КРИПТОВАЛЮТЫ!
Также можете посмотреть совершенно бесплатные наработки для МТ4, Квика, МТ5. Данный раздел также постоянно пополняется.
Не откладывайте свой шанс заработать на бирже уже сегодня!