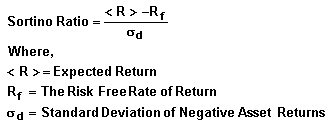Многие трейдеры и инвестиционные управляющие желают измерять и сравнивать результаты работы управляющих или отдельных торговых систем. Несмотря на то, что есть много способов измерить результат инвестирования, приведенная к риску доходность это одна из наиболее важных мер, поскольку, учитывая внутренне присущее фьючерсным рынкам плечо, большую доходность можно получить, взяв больше риска. Наиболее популярной мерой приведенной к риску доходности является коэффициент Шарпа. Несмотря на то, что коэффициент Шарпа используется наиболее широко, у него есть недостатки и ограничения. Из-за способа, которым вычисляется коэффициент Шарпа, он склонен наказывать положительную (upside) волатильность торговых результатов. Мы считаем, что коэффициент Сортино улучшает коэффициент Шарпа в некоторых моментах. Цель этой статьи – рассмотреть определение коэффициента Сортино и показать, как рассчитывать его правильно, поскольку очень часто это происходит некорректно.
Коэффициент Шарпа
Коэффициент Шарпа это метрика, целью которой является измерение успешности инвестиции путем деления избыточной по отношению к безрисковой ставке доходности на стандартное отклонение процесса, генерирующего эту доходность. Предложенный в 1966 году профессором финансов Стэнфордского Университета Уильямом Шарпом как мера результатов взаимных фондов, он, несомненно, дает некоторую оценку качества инвестирования, но имеет также некоторые ограничения.
Самый яркий его недостаток – он не различает отрицательную и положительную волатильность. Сильные положительные выбросы в серии результатов могут увеличить значение знаменателя (стандартного отклонения) на большую величину, чем значение числителя, таким образом уменьшая значение коэффициента Шарпа. Для некоторых распределений, имеющих положительную асимметрию результатов, таких как типичная тренд-следящая стратегия, коэффициент Шарпа может быть увеличен, если убрать наиболее большие положительные результаты. Это бессмыслица, поскольку инвесторы как правило рады большим позитивным результатам.
Большие позитивные отклонения являются признаком волатильности и риска, но если торговая стратегия последовательно дает сильные позитивные исходы и небольшие негативные исходы, она не должна быть наказана за эти сильные движения в свою пользу.
В случае, когда распределение результатов не является нормальным, коэффициент Шарпа дает сбои. Это в особенности неудачная метрика, когда сравниваются стратегии с положительной асимметрией, например тренд-следящие, со стратегиями с отрицательной асимметрией, например стратегии продажи опционов. В действительности, для положительно-асимметричных распределений доходность достигается с меньшим риском, чем это следует из коэффициента Шарпа. И наоборот, стандартное отклонение недооценивает риск для негативно-асимметричных распределений, то есть торговая стратегия более рискованна, чем это следует из коэффициента Шарпа. Типичная долгосрочная тренд-следящая стратегия, особенно с большим числом сделок, обычно имеет коэффициент Шарпа в диапазоне 0.5 — 0.9. Однако, негативно-асимметричная стратегия (возврата к среднему), например, продажа опционов, будет давать большой коэффициент Шарпа, 3.0 и выше, вплоть до разрушительной просадки. Коэффициент Шарпа часто не отражает внутренне присущий риск стратегий возврата к среднему.
Коэффициент Шарпа предполагает нормальное распределение и имеет склонность давать ложное чувство защищенности негативно-асимметричным стратегиям, которые устойчиво дают небольшие положительные результаты, но могут иметь редкие, болезненные сильные негативные исходы.
Коэффициент Сортино
Во многих случаях, коэффициент Сортино является лучшим выбором, особенно когда оцениваются и сравниваются результаты и стратегии управляющих с положительной асимметрией распределений результатов. Коэффициент Сортино является модификацией коэффициента Шарпа, использующей в качестве меры риска отрицательное отклонение вместо стандартного отклонения, то есть только те результаты, которые находятся ниже заданной пользователем цели (бенчмарка).
Интересно отметить, что даже нобелевский лауреат Гарри Марковиц (Harry Markowitz), когда он разработал Современную Теорию Портфеля (Modern Portfolio Theory, MPT) в 1959 году, признал, что, поскольку для инвесторов имеет значение только отклонения результатов вниз, использование их для измерения риска было бы более уместным, чем стандартное отклонение. Однако он все же использовал вариацию (корень из стандартного отклонения) в своей теории, поскольку оптимизации с использованием отрицательного отклонения были в его время непрактичными с вычислительной точки зрения.
В ранних 90-х, доктор Фрэнк Сортино (Frank Sortino) провел исследования и вывел улучшенную меру для приведенных к риску результатов. Согласно Сортино, это была идея Brian Rom из Investment Technologies назвать новую мерой коэффициентом Сортино. Первая ссылка на коэффициент была в журнале Financial Executive Magazine (август 1980), а первые высисления были опубликованы в серии статей в журнале Journal of Risk Management(сентябрь 1981).
Коэффициент Сортино определяется как:
Стандартное отклонение измеряет разброс данных относительно среднего значения, как выше, так и ниже него. Дельта (TDD) измеряет разброс данных ниже целевого определенного пользователем уровня, где все результаты выше целевого уровня полагаются нулевыми.
Пример расчета коэффициента Сортино
В этом примере, мы рассчитает годовой коэффициент Сортино для гипотетической торговой стратегии с положительной ассиметрией и следующим набором годовых результатов:
2%, 1%, –1%, 18%, 8%,–2%, 1%, –1%
Целевую доходность будем полагать равной 0%
Хотя в этом примере мы используем целевую доходность в 0%, любое значение может быть выбрано, в зависимости от цели управляющего. Конечно, разные значения цели приведут к разным значениям отклонений отрицательных значений. Если вы сравниваете управляющих или торговые системы, вы должны понимать, какое значение цели вам нужно использовать.
Сначала, посчитаем числитель в формуле для коэффициента Сортино:
Средний годовой результат – цель = 3.25% — 0% = 3.25%
Затем посчитаем TDD:
1) Для каждого элемента данных посчитаем разность между этим элементом данных и целевым уровнем. В нашем случае вычитать нечего и данные не изменятся.
2) Возведем каждый элемент данных в квадрат.
3) Посчитаем среднее значение для всех квадратов. Заметьте, что мы не «выбрасываем» нулевые значения:
Среднее = (0% + 0% + 0.01% + 0% + 0% + 0.04% + 0% + 0.01%) / 8 = 0.0075%
4) Возьмите квадратный корень из полученного в пункте 3 результата. Это TDD, знаменатель для формулы коэффициента Сортино.
TDD = sqrt(0.0075%) = 0.866%
Наконец, коэффициент Сортино = 3.25% / 0.866% = 3.75
Это довольно сильный результат. Вычисление коэффициента Шарпа для наших данных дало бы 0.52, довольно посредственное значение, где мы были наказаны за то, что в результатах содержится сильный положительный выброс.
Сортино против Сортино
Часто в литературе по трейдингу и в торговых программах мы видели коэффициент Сортино, который вычисляется неправильно. Чаще всего TDD вычисляется выбрасыванием всех нулевых элементов и взятием стандартного отклонения от оставшихся отрицательных элементов. Мы надеемся, что после чтения этой статьи вы видите, каким образом это неправильно.
Коэффициент Сортино учитывает и частоту результатов ниже цели, и их величину. Выбрасывая положительные элементы данных убирает чувствительность коэффициента к частоте отрицательных значений. Посмотрите следующие потоки сделок: [0, 0, 0, –10] и [–10, –10, –10, –10]. Выбросив нулевые значения из результатов мы получим одинаковые TDD для обоих потоков, но очевидно, что первый поток имеет гораздо меньший негативный риск, чем второй.
ПРИМЕР расчета Шарп и Сортино: https://cloud.mail.ru/public/YxqA/1KDwj9waD
Вы уже сейчас можете начать изучать Видео курс- роботы в TSLab и научиться самому делать любых роботов!
Можно записаться на следующий поток ОнЛайн курса «Создание роботов в TSLab без программирования», информацию по которому можно посмотреть тут->
Также можете научиться программировать роботов на нашем Видео курсе «Роботы для QUIK на языке Lua»
Если же вам не хочется тратить время на обучение, то вы просто можете выбрать уже готовые роботы из тех, что представлены у нас ДЛЯ TSLab, ДЛЯ QUIK, ДЛЯ MT5, ДЛЯ КРИПТОВАЛЮТЫ!
Также можете посмотреть совершенно бесплатные наработки для МТ4, Квика, МТ5. Данный раздел также постоянно пополняется.
Не откладывайте свой шанс заработать на бирже уже сегодня!