Анатолий Чернов
4 слагаемых успеха.
Говоря о трейдинге, можно выделить 4 слагаемых успеха – это:
— информация;
— анализ;
— самоконтроль;
— управление капиталом.
Самый лучший способ выигрывать в долгосрочной перспективе – это играть против своих ошибок. Если человек научится это делать, то, в конце концов, он достигнет успеха.
Вернемся снова к четырем слагаемым успеха.
Что касается информации – здесь все понятно. Надежность, полнота и оперативность информации изначально обеспечивают преимущество или отставание по отношению к остальным участникам торгов. Этот вопрос решается деньгами, на информации не стоит экономить, т.к. обычно потенциальные потери на порядок превышают затраты.
Анализ, как я уже указывал ранее, состоит из двух частей – создание «образа рынка» и его интерпретация. Создание образа – это вопрос, определяемый опытом трейдера и психологией. Что же касается интерпретации (технический анализ и т.п.), то все трейдеры в большей или меньшей степени умеют анализировать рынок. Вопрос ошибок анализа – это тема отдельной конференции, поэтому не буду его касаться в своем выступлении.
Самоконтроль – относится к психологии трейдинга. Этот вопрос также связан с «образом рынка» и сейчас рассматриваться не будет.
Я же хочу подробно остановиться на 4-ом пункте. Он связан с техническим контролем над рисками и управлением капиталом. На эту тему раньше многие трейдеры не обращали должное внимание, но при прочих равных условиях именно этот аспект делает максимальный вклад в общий долгосрочный успех. Поэтому в последние годы он все чаще и чаще притягивает внимание участников рынка.
Вопросы трейдера по управлению своим капиталом
С точки зрения управления капиталом хочу выделить три основных вопроса, которые задает себе трейдер:
— Когда входить в рынок?
— Когда выходить из позиции?
— Какое количество капитала вложить в сделку?
Что же такое – управление капиталом.
В свете этих вопросов с точки зрения математики можно определить управление капиталом как поиск оптимального решения в пространстве доход-риск.
Что здесь я понимаю под риском? Когда говорится о технологиях управления портфелем, то под риском, как правило, понимается риск предсказуемости по управлению (т.е. риск отклонения от среднестатистического результата). Таким образом, сводится к минимуму отклонение доходности портфеля от базовой. Но при этом не учитывается тот факт, что базовая доходность может быть отрицательной (если «рынок упадет»).
Поэтому я буду говорить о реальном риске – риске потери капитала, связанного с неблагоприятным движением цен.
Рассмотрим функцию, которая определяет прирост капитала за один торговый цикл: открытие/закрытие позиции.
M = Cap1/Cap0
Теперь определим положительное и отрицательное изменение капитала.
M+ = 1 + f * d+
M– = 1 + f * d–
В данных формулах:
f – это доля капитала, участвующая в сделке,
d+, d– – это, соответственно, приведенные доход/потери с учетом комиссии и проскальзывания.
Показатели d немного отличаются по своей структуре для срочного рынка и рынка с плечом (например, рынок Форекс или рынок акций).
При расчете этих показателей к изменению цены добавляется поправка на «проскальзывание» при открытии/закрытии позиции и комиссионные расходы.
Вопрос комиссии и «проскальзывания» очень важен. Если провести несложные подсчеты, то выясняется, что комиссия достаточно сильно снижает вероятность выигрыша, особенно если мы рассматриваем внутридневной трейдинг (дейтрейдинг).
Теперь рассмотрим формулы для d. Начнем со срочного рынка.
d = r * S / (Z + com), где
r – доход с 1 контракта при движении равном 1 пункту,
Z – залог за 1 контракт,
com – комиссионные расходы (фиксированные или в % от цены),
S+ = Сдвиг цены – com – проскальзывание,
S— = Сдвиг цены – com – проскальзывание.
Рынок, где разрешена торговля с использованием плеча.
d = L * S / (Price + com) , где
Price – цена открытия позиции,
L – величина «плеча» или «рычаг», остальное совпадает с предыдущим случаем.
Изменение капитала как математическое ожидание.
А теперь немного статистики. Пусть мы проводим N торговых циклов с одинаковыми параметрами d+, d–, p (вероятность выигрыша).
Тогда вероятность того, что из N торговых циклов k будут успешными:
Pk = pk * (1-p)N-k * N! / (k! * (N—k)!)
Перейдем к рассмотрению математического ожидания изменения капитала. Если количество операций со сходными параметрами устремить к бесконечности, то согласно теореме Бернулли математическое ожидание изменения капитала за одну операцию можно представить в таком виде:
M = M+P * M–1-P, где
P – средняя частота выигрыша (фактически, вероятность выигрыша).
Здесь сделано первое допущение. Оно имеет определенные границы корректности, о которых мы поговорим позже. Но для того, чтобы показать качественную картину, этого вполне достаточно. А потом мы попробуем более корректно отнестись к сделанному допущению.
Поиск оптимальной доли капитала, участвующей в сделке.
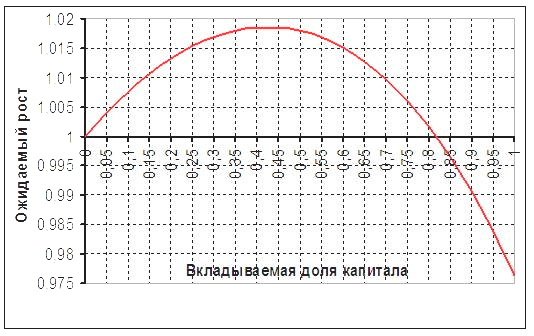
Если построить график зависимости ожидаемого прироста М от доли капитала, участвующего в сделке, то получается следующая кривая.
Отсюда видно, что действительно существует теоретический максимум f. Вопрос только в том, в какой зоне шкалы Х он лежит.
Параметр f теоретически может принимать отрицательные и положительные значения (как в интервале от 0 до 1, так и выше).
Если, например, f принимает значения в интервале от 0 до 1, то здесь все просто. Это действительно доля от полного капитала, который можно вложить в сделку. Если f больше единицы, это случай, когда «плечо» слишком мало для достижения оптимального результата.
Случай, когда f меньше нуля, разбивается на два варианта. В первом, когда f значительно меньше нуля, нужно открывать позицию в противоположную сторону. Но есть и второй – для небольших отрицательных f. В этом случае нередко возникает ситуация, когда открытие позиции в любую сторону является невыгодным. Подобная ситуация появляется как раз за счет того, что есть комиссионные расходы и «проскальзывание».
В принципе, любой желающий может легко дома воспроизвести эту модель и увидеть описанные мною границы на любой собственной статистике.
В своем выступлении я приведу пример поиска максимума функции прироста капитала решения для простейшего случая, когда у нас есть только два исхода (в результате трейда капитал может либо вырасти, либо упасть). Найдем fMAX такое, что M = MMAX
f = fMAX = P/(-d–) – (1-P)/d+
При f = fMAX функция роста капитала примет значение
MMAX = PP * ((1-P)/K)1-P * (K+1), где
K = d+ / (-d–) – это соотношение между относительными положительным и отрицательным сдвигами, скорректированными с учетом комиссии и проскальзывания.
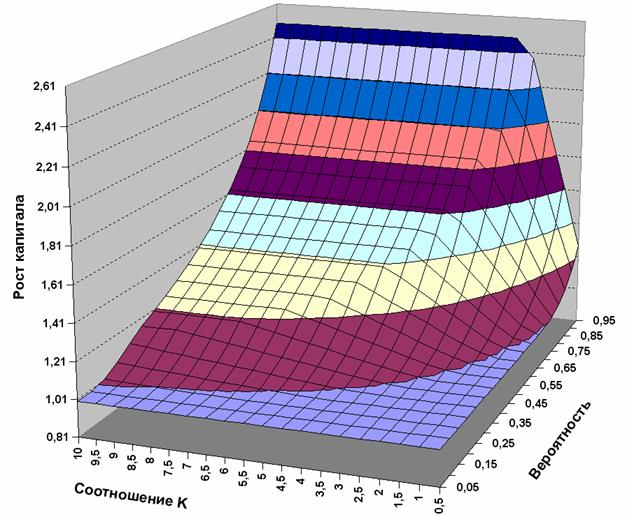
Если построить поверхность по значениям MMAX в зависимости от P и K, то получится достаточно любопытная картинка (см. рис), из которой можно сделать несколько выводов. Все эти выводы связаны с границами успешной торговли.
Если провести анализ функции fMAX, с учетом 0 < fMAX <= 1 и MMAX >= 1, то получим:
P > 1 / (K + 1)
P <= (1+d+) / (K+1)
Наиболее важным является первое неравенство, которое определяет зону положительных решений.
Второе же неравенство – это скорее ограничитель, связанный с тем случаем, когда мы предполагаем, что fMAX не больше 1.
Что осталось «за кадром»?
А теперь несколько слов о том, что не было учтено.
Я привел пример для двух исходов, а в реальности их может быть несколько.
Что значит два исхода? Предположим, есть простейшая торговая система, например, какое-нибудь пересечение цены и ее скользящего среднего, которое дает сигнал на покупку, либо на продажу. Это классический пример двух исходов. Если торговая система немного сложнее, то появляются 3 и больше исходов.
Например, торговая система может давать нейтральный сигнал или, например, торговая система, основанная на ближайших уровнях поддержки сопротивления, там, где присутствуют один исход типа «stop loss» и еще два исхода фиксации прибыли на двух ближайших уровнях сопротивления. Чуть позже поговорим о том, как в этом может выглядеть ожидаемый прирост капитала.
Не учтена ошибка оценки вероятности.
Этот момент связан как с допущением о корректности использования теоремы Бернулли, так и с корректной интерпретацией средней частоты выигрыша. Действительно, при больших N можно сделать это допущение, но нужно предположить, что распределение близко к Гауссовому, и учесть влияние стандартного отклонения. Об этом подробнее поговорим дальше.
Не учитывалось возможное отклонение от ожидаемого движения.
Далеко не всегда величины приведенного дохода/потерь можно точно оценить, обычно ожидания находятся в диапазоне, в котором есть определенные их распределения.
Кстати, если говорить о распределениях, то я рекомендовал бы больше обращать внимание на логарифмические нормальные распределения, либо на параметрические неравносторонние распределения, а не на классические нормальные (гауссовы). Это связано с тем, что, строго говоря, распределение изменения капитала в процентах (а также иных подобных величин) имеет фиксированную левостороннюю границу (-100%), а правосторонняя – неограниченна. Подобное наблюдается для вероятности, только в этом случае фиксированы обе границы 0 и 1.
Не рассмотрен случай «сигнальных» систем (без ориентиров d+, d–).
Из предыдущих двух замечаний вытекает, что случай «сигнальных» систем (два исхода) требует специального уточнения, т.к. он связан с большими стандартными ошибками по вероятности и, особенно, по приведенным доходам/потерям d.
Для примера дальше продемонстрирую, как можно произвести учет некоторых ошибок. Сразу отмечу, что в приведенных оценках не все допущения идеально корректны, но для того, чтобы увидеть качественную общую картину, их будет вполне достаточно.
Предположения следующие:
для каждого исхода можно определить вероятность и приведенный доход, можно использовать Гауссового распределение (это как раз не очень корректно, т.к. там несколько иное распределение, но чтобы не усложнять сильно формулы, я не стану приводить этот вариант).
Математическое ожидание роста капитала для случая N исходов.
Формула, в принципе, похожа на ту, что мы видели в случае 2-х исходов, только здесь произведение N исходов.
M = Пk=1, N(MkPk),где
П – функция произведения (N множителей)
Pk – вероятность k-го исхода
Mk – рост капитала для k-го исхода
Учет ошибки оценки вероятности.
Для учета ошибки оценки вероятности применим осреднение (с учетом гауссовой функции распределения для вероятности). В результате в формуле ожидаемой прибыли появляется поправочный множитель (обычно он близок к 1, отличаясь на несколько процентов).
MER = M * Пk=2,N(Аk)
Пk=2,N(Аk) – это произведение корректирующих функций, рассмотрим их приблизительный вид:
Аk = (Mk/M1)tk/2 * Gk,где
M1 – наименьшее значение из всех Mk
tk – поправка по степени
tk =Dk * ln(Mk/ M1) , где Dk – дисперсия Pk
Самый простой вариант для двух исходов, когда
t = D * ln(M+/M–)
Gk – поправка на интервал, для случая двух исходов будет выглядеть так
G = (Г1-Г2) / (Г01-Г02), где
Г – гамма-функция, интегральная форма нормального распределения
Г1=Г((1-P—t) / (2*D)0,5)
Г2= Г((-P—t) / (2*D)0,5), где Г01 и Г02 – равны Г1 и Г2 при t = 0
G – поправочный коэффициент, который возникает из Гауссового распределения, фактически представляет собой некую функцию от интегральных функций нормального распределения.
Сравнение «до» и «после» учета ошибки.
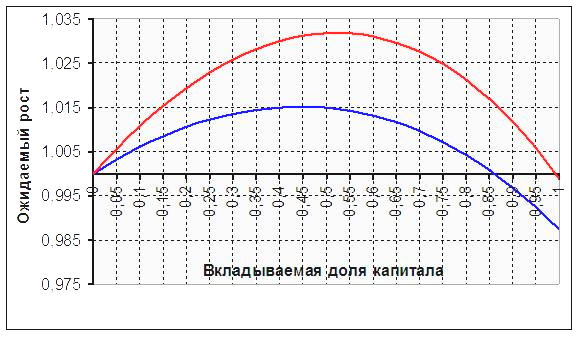
Снова рассмотрим график зависимости ожидаемого прироста М от доли капитала, участвующего в сделке. Что изменилось после учета ошибки по сравнению с идеальным случаем?
Красная линия показывает, что было для случая двух исходов без учета ошибки. Синяя линия – после учета ошибки.
При расчете синей линии рассматривался случай, когда вероятность выигрыша больше, чем вероятность проигрыша, соотношение же приведенного дохода/потерь было достаточно близким. Видно, что поправки на ошибки уменьшают значение оптимальной доли капитала и приводят к уменьшению математически ожидаемой прибыли.
Учет ошибки оценки приведенного дохода/потерь.
Не буду приводить здесь сложных формул, т.к. их вид нам не поможет понять влияние ошибки, а только запутает. Хочу лишь отметить, что если рассматривать аналогичное осреднение по смещению, то будет наблюдаться картина, схожая с предыдущим случаем. Т.е. происходит уменьшение оптимальной доли капитала (точка максимума) и снижение ожидаемой прибыли.
Статистический критерий совершения сделки.
Теперь вернемся к теме уменьшения собственных ошибок. В принципе, у каждой торговой системы есть показатели выигрыша-проигрыша. Каждая система имеет сильные и слабые места. Можно попробовать уменьшить последствия слабых мест системы, если постараться использовать кроме обычного следования сигналам статистический фильтр, который позволит отсеивать наиболее рискованные сделки. Об этом мы сейчас поговорим.
Рассмотрим классическую формулу дисперсии в применении к функции прироста капитала:
DM = M2 – M2
Дисперсия равна среднеквадратичному за вычетом квадрата от арифметического среднего. Стандартное отклонение – квадратный корень из дисперсии.
Теперь сформулируем Критерий фильтрации низкорентабельных сделок. Величина математического ожидания прироста капитала за один торговый цикл должна превышать в некоторое количество раз (большее или равное единице) величину стандартного отклонения:
(M2 / DM ) > X >= 1
Как выбрать это количество (X) – личное дело каждого трейдера. Все определяет его желание рисковать. В качестве ориентира могут привести некоторые значения из теории статистики. Например, если у нас нормальное (гауссово) распределение, где Х равен единице, то с вероятностью порядка 70% будут фильтроваться ошибки. Если хочется увеличить эту вероятность до 95%, нужно использовать два стандартных отклонения (Х=2). А три стандартных отклонения уже обеспечат вероятность успешной фильтрации ошибок больше 99%. Естественно, применение фильтра приведет к уменьшению количества сделок, но зато повысится их качество.
В завершение темы рассмотрим пример расчета статистического фильтра на основе предыдущих формул (с «учетом ошибки»):
Пk=2,N ((Mk/M1)tk * G1k) < (X+1)/X <= 2
Возможные пути оценки параметров функции роста капитала на реальных данных/
В заключение хочу рассказать, как реально все это можно применять на практике. Тема достаточно сложная и требует отдельных исследований, поэтому остановимся на ней очень кратко.
Возможны два типа действий:
— Анализ результатов торговой системы при близких условиях.
— Построение функции на основе создания методики численной оценки результатов технического анализа.
Рассмотрим подробнее первый вариант. У нас есть некая торговая система, есть ее результаты. Исходя из этих результатов, в принципе, можно построить некую статистическую параметрическую модель, которая будет с определенной достоверностью давать результат, и подсчитать оптимальную долю капитала fMAX.
Здесь хотелось бы подчеркнуть один важный момент. Обычно для качественного функционирования торговой системы не хватает только сигналов, приходящих от системы. Нужно еще оценивать состояние рынка.
Дело в том, что у каждой системы есть ограниченная область применения. При различных состояниях рынка она дает разную эффективность. Поэтому я бы рекомендовал предварительно провести анализ рынка во всех ситуациях, когда приходил сигнал от торговой системы и затем провести обычный регрессионный многопараметрический анализ с целью выделить те критерии оценки состояния рынка, которые дают маленькую наибольшую эффективность.
Далее можно легко распределить общее количество сделок по группам, соответствующим различным типам состояний рынка. И, соответственно, производить исследования по оптимальному f, по каждой группе.
Таким образом, при приходе сигнала от торговой системы мы должны будем предварительно оценить состояние рынка, а уже затем найти оптимальное f, и принять решение о сделке, руководствуясь статистическим критерием. При этом можно очень значительно увеличить успешность работы и, соответственно, уменьшить ошибки.
Это достигается путем введения переменных коэффициентов. Что же касается применения портфеля систем, то его использование, конечно, увеличивает предсказуемость (если там собраны системы, результаты которых антикоррелируют между собой). Но, к сожалению, выполнение условия антикоррелированности не всегда возможно, поэтому эффективнее применять одну систему, но с фильтрацией потенциально ошибочных сделок.
Что касается второго варианта, то он тоже достаточно интересен, т.к. не учитывает эффективность предыдущей работы системы, а пытается прогнозировать будущее. Он может использоваться теми, кто пытается как-то сигналы технического анализа перевести в строгую математическую форму (например, с помощью методики «распознавания образов» и подобных).
В свое время проводил интересные эксперименты, которые позволяли сказать то, что подобный подход можно применять, когда каждый сигнал оценивается 3-4 степенями градации и строится система из большого количества сигналов разных типов (включая оценку состояния рынка).
Например, строил систему из порядка 250 показателей (сигналов) и она давала с учетом этой методики достаточно хорошие показатели отсеивания потенциально неуспешных сделок (чтобы вас не смущать я не стану приводить численные результаты ее эффективности, которые превышали 70%). Единственная проблема была в том, что на тот момент не удалось формализовать некоторые сигналы. Поэтому использование такого подхода требовало каждый раз многочасовые предварительные расчеты, что не очень удобно для активного трейдинга. Поэтому хочу пожелать вам создать более удобные и быстрые модели.
Вы уже сейчас можете начать изучать Видео курс- роботы в TSLab и научиться самому делать любых роботов!
Можно записаться на следующий поток ОнЛайн курса «Создание роботов в TSLab без программирования», информацию по которому можно посмотреть тут->
Также можете научиться программировать роботов на нашем Видео курсе «Роботы для QUIK на языке Lua»
Если же вам не хочется тратить время на обучение, то вы просто можете выбрать уже готовые роботы из тех, что представлены у нас ДЛЯ TSLab, ДЛЯ QUIK, ДЛЯ MT5, ДЛЯ КРИПТОВАЛЮТЫ!
Также можете посмотреть совершенно бесплатные наработки для МТ4, Квика, МТ5. Данный раздел также постоянно пополняется.
Не откладывайте свой шанс заработать на бирже уже сегодня!